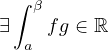Teorema 1.1 (Unicitá del limite). Sia αβ ∈ℝ.
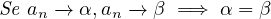
Teorema 1.5 (TSM Successioni monotone).
| Se (an) ↗ | 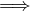 ∃limn→∞an = supn∈ℕ(an) ∃limn→∞an = supn∈ℕ(an) | ||
| Se (an) ↘ |  ∃limn→∞an = inf n∈ℕ(an) ∃limn→∞an = inf n∈ℕ(an) |
Siano A ⊆ℝN f : A →ℝM α ∈ D(A)λμ ∈ℝM( se M = 1)
Teorema 2.4 (TLM Limite delle funzioni monotone). Sia x0 ∈ℝM f ↗
| Se x0 ∈ D(Ax0-) | 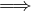 f(x) f(x)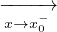 supAx
0-f supAx
0-f | ||
| Se x0 ∈ D(Ax0+) | 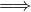 f(x) f(x)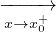 inf Ax
0-f inf Ax
0-f | ||
| Se + ∞∈ D(A) | 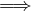 f(x) f(x)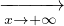 supAf supAf | ||
| Se -∞∈ D(A) | 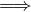 f(x) f(x)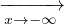 inf Af inf Af |
dove Ax0- := A ∩ ]-∞,x0[Ax0+ := A ∩ ]x0,+∞[. Un risultato analogo vale per f ↘
Teorema 3.1 (CSC Caratterizzazione sequenziale della continuitá). Sia x0 ∈ A. Siano A ⊆ ℝN f : A →ℝM x0 ∈ A.
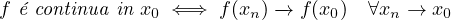
Sia I un intervallo di ℝ.
Teorema 3.3 (TVI Valore intermedio). Sia f ∈ C(I,ℝ).
| Dato y ∈ℝ : f(a) < f(y) < f(b) | 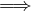 ∃x0 ∈ I : f(x0) = y ∃x0 ∈ I : f(x0) = y | ||
| f(I) | é un intervallo |
Teorema 4.4 (TM Test monotonia). Sia I un intervallo su ℝ, f : I →ℝ derivabile in I.
| f′(x) = 0 ∀x ∈ I | ⇐⇒ f é costante in I | (1) |
| f′(x) ≥ 0 ∀x ∈ I | ⇐⇒ f ↗ | (2) |
| f′(x) > 0 ∀x ∈ I |  f ↗ s. f ↗ s. | (3) |
| f ↗ s. | ⇐⇒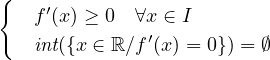 | (4) |
Teorema 4.5 (Taylor con resto di Peano). Siano I intervallo di ℝ x0 ∈ I f derivabile n volte in x0. Allora
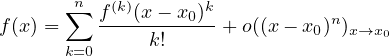
Teorema 4.6 (Tayor con resto di Lagrange). Siano I intervallo aperto di ℝ x0 ∈ I f derivabile n volte in x0. Allora ∀x ∈ I ∃yx ∈ (x0,x) tale che

Teorema 4.7 (TH De l’Hópital). Siano I intervallo di ℝ x0 ∈ D(I)f,g : I \{x0} → ℝ derivabili in
I \{x0} con g′(x)≠0 ∀x ∈ I \{x0}. f(x)g(x)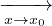 0 o |g(x)|
0 o |g(x)|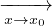 + ∞. Allora
+ ∞. Allora
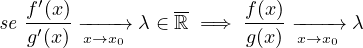
Teorema 4.10. Sia f ∈ Cn+1(I,ℝ), x0 ∈I∘ con f(k)(x0) = 0 per k ≤ n e f(n+1)(x0)≠0. Allora
| x0 é un punto di massimo locale forte di f se (n+1) é pari e f(n+1)(x 0) < 0 | |||
| x0 é un punto di minimo locale forte di f se (n+1) é pari e f(n+1)(x 0) > 0 | |||
| x0 non é un punto estremante se (n+1) é dispari |
Teorema 5.1. Sia f : [a,b] →ℝ limitata e c ∈ ]a,b[.
| Se f ∈ C([a,b],ℝ) |  f ∈ R[a,b] f ∈ R[a,b] | ||
| Se f é monotona |  f ∈ R[a,b] f ∈ R[a,b] | ||
| {x ∈ [a,b]∕f non é continua in x}é finito |  f ∈ R[a,b] f ∈ R[a,b] | ||
| f ∈ R[a,c] f ∈ R[c,b] | ⇐⇒ f ∈ R[a,b] |
Teorema 5.3 (1TFC Primo teorema fondamentale del calcolo). Siano f ∈ R[a,b] F(X) = ∫ axf(t)dt : [a,b] →ℝ. Allora
| F | ∈ C([a,b],ℝ) | ||
| Se f é continua in x0 |  f(x0) = F′(x0) f(x0) = F′(x0) |
Teorema 5.4 (2TFC Secondo teorema fondamentale del calcolo). SIano f ∈ R[a,b] e Φ una primitiva di f. Allora
![∫ b
f(t)dt = [Φ(t)]b = Φ(b) - Φ(a)
a a](b_formulario_analisi_1_mon49x.png)
Siano a ∈ℝ β ∈ℝ a < β f ∈ C([a,β[,ℝ).
Teorema 6.4 (CFO Criterio delle funzioni oscillanti). Sia f ∈ C([a,β[,ℝ) : f abbia una primitiva limitata in [a,β[, g ∈ C1([a,β[,ℝ) : g ↘x→β-0. Allora