-
N(t) = N(0)e-λt Legge di decadimento radioattivo (t tempo,λ probabilitá di decadimento dei
nuclei nell’intervallo di tempo)
-
H(t′) = ∑
HiCieλit′ Produzione di calore della roccia al tempo t’, Ci le concentrazioni dei
nuclei radioattivi
-
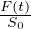 =
= 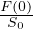 +
+ 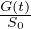 [eλt - 1] Isocrona di roccia intera
[eλt - 1] Isocrona di roccia intera
-
yi = c + xi[eλt - 1]
-
T(z) = -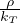 H
H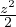 +
+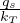 z+Ts Temperatura in funzione della profonditá dalla legge di conduzione
stazionaria per valori di H costanti
z+Ts Temperatura in funzione della profonditá dalla legge di conduzione
stazionaria per valori di H costanti
-
Ti(z) = -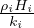
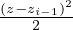 +
+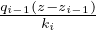 +Ti-1 Generalizzazione della precedente per un sistema
multistrati dove teniamo in considerazione la continuitá della temperatura (T+ = T-) e la
continuitá del flusso di calore (q+ = q-) fra gli strati dove gli indici i - 1 indicano l’ultimo
valore assunto dallo strato precedente
+Ti-1 Generalizzazione della precedente per un sistema
multistrati dove teniamo in considerazione la continuitá della temperatura (T+ = T-) e la
continuitá del flusso di calore (q+ = q-) fra gli strati dove gli indici i - 1 indicano l’ultimo
valore assunto dallo strato precedente
-
Per crosta terrestre H(z) = H0e-z∕δ ovvero k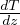 = ρδH0e-z∕δ + c
1 dove avendo assunto
h >> δ possiamo dire che c≈qm da cui ricaviamo contributo crostale qs = qm+qc = qm+[ρH]δ
da cui otteniamo
= ρδH0e-z∕δ + c
1 dove avendo assunto
h >> δ possiamo dire che c≈qm da cui ricaviamo contributo crostale qs = qm+qc = qm+[ρH]δ
da cui otteniamo
-
T(z) = Ts + 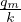 z +
z + 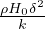 (1 - e-z∕δ) Geoterma continentale
(1 - e-z∕δ) Geoterma continentale
-
q(r) = 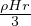 Flusso alla distanza r dal centro del pianeta per pianeta sferico con r dell’o.d.g del
raggio del pianeta
Flusso alla distanza r dal centro del pianeta per pianeta sferico con r dell’o.d.g del
raggio del pianeta
-
T(r) = Ts+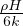 (a2-r2) Temperatura alla distanza r per pianeta sferico (a raggio del pianeta)
(a2-r2) Temperatura alla distanza r per pianeta sferico (a raggio del pianeta)
-
T(z,t) = ℜ{Z(z)f(t)} = ℜ{(ΔTe-z∕δe-iz∕δ)(eiωt)} = ΔTe-z∕δcos(ωt -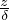 ) Riscaldamento
periodico di un semispazio da sorgente esterna dove abbiamo definito δ =
) Riscaldamento
periodico di un semispazio da sorgente esterna dove abbiamo definito δ = 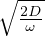 lo spessore di
penetrazione
lo spessore di
penetrazione
-
T(z,t) = Ts+(T0-Ts)erf(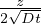 ) Raffreddamento istantaneo di un semispazio a Temperatura
T0 posto a contatto con un termostato Ts dove erf é la Error function erf(η) =
) Raffreddamento istantaneo di un semispazio a Temperatura
T0 posto a contatto con un termostato Ts dove erf é la Error function erf(η) = 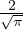 ∫
0ηe-t2
dt
∫
0ηe-t2
dt
-
q(z,T) = 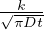 (T0 - Ts)e-η2
=
(T0 - Ts)e-η2
= 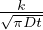 (T0 - Ts)e-
(T0 - Ts)e-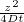 Flusso di calore del raffreddamento
istantaneo, ottenuto da q = k
Flusso di calore del raffreddamento
istantaneo, ottenuto da q = k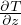 = k
= k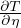
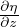 essendo η =
essendo η = 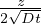
-
t = 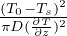 ≈ 6 × 106anni Stima dell’etá della Terra di Kelvin eguagliando il flusso di calore
q = k
≈ 6 × 106anni Stima dell’etá della Terra di Kelvin eguagliando il flusso di calore
q = k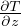 al flusso del raffreddamento istantaneo
al flusso del raffreddamento istantaneo
-
T(z,t) = Ts + (T0 - Ts)erf(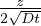 ) Geoterma oceanica nel sistema di riferimento solidale con
la litosfera in movimento (stesso risultato del raffreddamento istantaneo)
) Geoterma oceanica nel sistema di riferimento solidale con
la litosfera in movimento (stesso risultato del raffreddamento istantaneo)
-
T(z,x) = Ts + (T0 - Ts)erf(
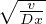 ) Geoterma oceanica nel sistema di riferimento fermo
rispetto alla dorsale, essendo v la velocitá di deriva della litosfera rispetto alla dorsale, x
la distanza percorsa dall’origine, da cui si puó derivare flusso di calore analogo a quello del
semispazio
) Geoterma oceanica nel sistema di riferimento fermo
rispetto alla dorsale, essendo v la velocitá di deriva della litosfera rispetto alla dorsale, x
la distanza percorsa dall’origine, da cui si puó derivare flusso di calore analogo a quello del
semispazio
-
zL = 2.32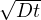 = 2.32
= 2.32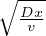 Spessore della Litosfera dato dall’aver compiuto il 90%
dell’escursione termica
Spessore della Litosfera dato dall’aver compiuto il 90%
dell’escursione termica
-
w = 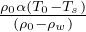 2
2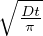 Topografia isostatica dei fondali oceanici (essendo w la profonditá del
fondale rispetto alla quota della sommitá della dorsale), derivata dal principio di isostasia
Topografia isostatica dei fondali oceanici (essendo w la profonditá del
fondale rispetto alla quota della sommitá della dorsale), derivata dal principio di isostasia
-
h = 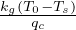 stima dell’altezza di un ghiacciaio trascurando avvezione e depositi di ghiaccio
(stima irrealistica), sono noti T0eTs temperatura alla base e temperatura esterna
stima dell’altezza di un ghiacciaio trascurando avvezione e depositi di ghiaccio
(stima irrealistica), sono noti T0eTs temperatura alla base e temperatura esterna
-
T(z) = Ts + 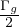
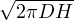 a(1 - erf(u(z))) = Ts +
a(1 - erf(u(z))) = Ts + 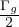
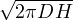 a(1 - erf(
a(1 - erf(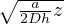 ))) temperatura
in un ghiacciaio a base fredda da cui considerando la bse vicina al punto di fusione
))) temperatura
in un ghiacciaio a base fredda da cui considerando la bse vicina al punto di fusione
Tf = Ts + 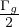
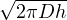 a che ci permette di stimare l’altezza del ghiacciaio a h = (
a che ci permette di stimare l’altezza del ghiacciaio a h = (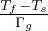 )2
)2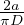 piú realisticamente
piú realisticamente
-
A′i1i2...ik = Ci1j1Ci2j2...CikjkAi1i2...ik Definizione di tensore
-
δij Delta di Kronecker (δij = 1 quando i = j, 0 altrove)
-
eijk Tensore di Ricci (eijk = 1 per permutazioni pari di 123, -1 per permutazioni dispari, 0
altrove)
-
eijkeklm = δilδjm - δimδjl Identitá e - δ
-
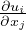 = εij+ωij Gradiente dello spostamento diviso in componente simmetrica e antisimmetrica
= εij+ωij Gradiente dello spostamento diviso in componente simmetrica e antisimmetrica
-
εij = 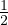 (
(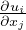 +
+ 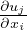 ) Tensore infinitesimo di deformazione
) Tensore infinitesimo di deformazione
Nel sistema di riferimento degli autovettori normalizzati la variazione relativa lungo la
componente i é il valore εii = 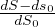 , viceversa con i≠j εij =
, viceversa con i≠j εij = 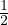 (α +β) angoli di deformazione
nel piano
(α +β) angoli di deformazione
nel piano
-
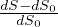 = εij
= εij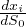
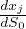 Variazione relativa di distanza fra due punti distanti dxi
Variazione relativa di distanza fra due punti distanti dxi
-
εkk = ∇⋅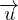 =
= 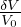 Traccia del tensore é variazione volumetrica relativa
Traccia del tensore é variazione volumetrica relativa
-
εij(I) = 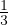 εkkδij Componente isotropa tensore deformazione
εkkδij Componente isotropa tensore deformazione
-
ε′ij = εij -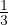 εkkδij Componente deviatorica tensore deformazione
εkkδij Componente deviatorica tensore deformazione
-
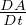 = ∫
V (t){
= ∫
V (t){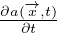 + ∇⋅ [a(
+ ∇⋅ [a(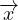 ,t)
,t)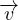 ]}dV Derivata di grandezze additive A dove a(
]}dV Derivata di grandezze additive A dove a(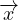 ,t) é la
densitá di A e il prodotto a
,t) é la
densitá di A e il prodotto a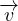 il flusso di A
il flusso di A
-
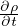 + ∇⋅ (ρ
+ ∇⋅ (ρ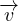 ) = 0
) = 0
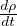 + ρ∇⋅
+ ρ∇⋅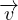 = 0 Equazione di continuitá (dalla conservazione della massa)
= 0 Equazione di continuitá (dalla conservazione della massa)
-
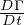 = ∫
V (t)ρ
= ∫
V (t)ρ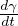 dV Applicazione dell’equazione di continuitá a grandezze Γ dipendenti dalla
massa
dV Applicazione dell’equazione di continuitá a grandezze Γ dipendenti dalla
massa
-
Ti(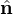 ) = nkτki Trazione su una superficie di normale n note le componenti τki
) = nkτki Trazione su una superficie di normale n note le componenti τki
-
fi + 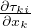 = ρ
= ρ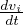 Equazioni del moto
Equazioni del moto
-
τij = τji Dall’equazione del momento angolare
-
p = -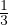 τkk Pressione media dovuta agli sforzi normali
τkk Pressione media dovuta agli sforzi normali
-
σ′1 = σ1 -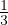 τkk
τkk
σ′2 = σ2 -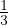 τkk
τkk
σ′3 = σ3 -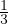 τkk
τkk
-
Smax = 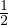 (σmax - σmin) Sforzo di taglio massimo
(σmax - σmin) Sforzo di taglio massimo
-
0 = ρgδi3 + 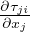 Stato di sforzo in prossimitá della superficie della crosta
Stato di sforzo in prossimitá della superficie della crosta
-
τij = Δτij -plitδij Ambienti tettonici, Δτij fornisce la componente deviatorica
σ′i = σi + p
τ′kk = 0 ⇐⇒ σ′1 + σ′2 + σ′3 = 0
σ′z = σ′1 Ambiente distensivo, faglia normale
σ′z = σ′3 Ambiente compressivo, faglia inversa
σ′z = σ′2 Faglia trasforme, compressione e distensione sul piano xy
-
tan(2β) = 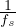 Teoria della fagliazione di Anderson avendo fs > 0 coefficiente di attrito statico
Teoria della fagliazione di Anderson avendo fs > 0 coefficiente di attrito statico
δ = 90 - β > 45 Ambiente distensivo, faglia normale
δ = β < 45 Ambiente compressivo, faglia inversa
Per faglia trasforme β < 45 angolo fra piano ed asse di massima compressione
-
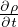 +
+ 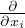 (ρvi) = 0 Equazione di continuitá
(ρvi) = 0 Equazione di continuitá
-
ρ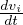 = fi +
= fi + 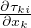 i = 1,2,3 Equazioni del moto
i = 1,2,3 Equazioni del moto
-
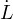 =
= 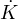 + ∫
Bτij
+ ∫
Bτij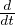 εijdV =
εijdV = 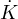 +
+ 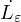 Equazione dell’energia per un continuo
Equazione dell’energia per un continuo
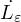 = ∫
Bτij
= ∫
Bτij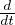 εijdV Lavoro di deformazione
εijdV Lavoro di deformazione
Δ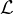 ε = τjiΔεij Variazione nell’intervallo Δt
ε = τjiΔεij Variazione nell’intervallo Δt
Δ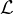 ε = Δ
ε = Δ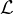 V + Δ
V + Δ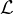 F Lavoro di deformazione su dV
F Lavoro di deformazione su dV
Δ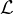 V = -p
V = -p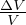 Lavoro speso per cambiare il volume
Lavoro speso per cambiare il volume
Δ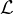 F = τ′ijΔε′ij Lavoro speso per cambiare la forma a V costante (τij = pδij + τ′ij)
F = τ′ijΔε′ij Lavoro speso per cambiare la forma a V costante (τij = pδij + τ′ij)
-
F = kΔu Legge di Hooke
-
τij = Cijklεkl Relazione costitutiva che lega τij ad εij (21 costanti libere)
τij = λεkkδij + 2μεij Relazione costitutiva per materiale isotropo (λ,μ costanti di Lamé)
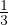 τkk = Kεkk = -Δp Legame parti isotrope, K incompressibilitá, bulk modulus
τkk = Kεkk = -Δp Legame parti isotrope, K incompressibilitá, bulk modulus
τ′ij = 2με′ij Legame parti deviatoriche, μ rigiditá, shear modulus
K = λ + 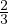 μ
μ
K = 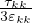 = -V
= -V 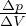
KT = -V (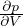 )T Incompressibilitá isoterma
)T Incompressibilitá isoterma
KS = -V (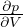 )S Incompressibilitá adiabatica
)S Incompressibilitá adiabatica
-
εij = 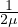 (τij - λεkkδij) Relazione costitutiva inversa, deformazione dato lo sforzo εkk =
τkk∕(3λ + 2μ)
(τij - λεkkδij) Relazione costitutiva inversa, deformazione dato lo sforzo εkk =
τkk∕(3λ + 2μ)
εij = 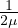 (τij -
(τij -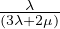 τkkδij)
τkkδij)
-
τkk = τ11 Stato di sforzo uniassiale
E = 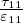 = μ
= μ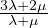 Modulo di Young, trazione su allungamento relativo
Modulo di Young, trazione su allungamento relativo
ν = -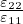 =
= 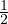
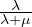 Modulo di Poisson, contrazione trasversale sulla variazione relativa
longitudinale
Modulo di Poisson, contrazione trasversale sulla variazione relativa
longitudinale
-
ρ0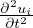 = fi +
= fi + 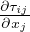 Equazione del moto per piccole deformazioni
Equazione del moto per piccole deformazioni
-
ρ0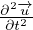 =
= 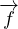 + (λ + μ)(∇(∇⋅
+ (λ + μ)(∇(∇⋅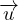 )) + μ∇2
)) + μ∇2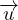 Equazione di Cauchy-Navier per le onde elastiche
Equazione di Cauchy-Navier per le onde elastiche
-
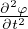 = c2∇2φ Equazione d’onda di D’Alembert, c velocitá di propagazione dell’onda
= c2∇2φ Equazione d’onda di D’Alembert, c velocitá di propagazione dell’onda
ϕ = ∇⋅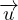 = εkk Onde P (Primae), longitudinali
= εkk Onde P (Primae), longitudinali
V P = 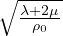 Velocitá onde P
ψ = ∇×
Velocitá onde P
ψ = ∇×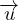 Onde S (Secundae), trasversali
Onde S (Secundae), trasversali
V S = 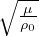 Velocitá onde S
Velocitá onde S
-
Fluidi Viscosi Newtoniani
F = η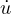 Pistone,
Pistone, 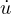 velocitá del pistone
velocitá del pistone
εij(I) Deformazione isotropa limitata
ε′ij Deformazione deviatorica illimitata
σij Sforzo dovuto al moto del fluido (0 quando fluido in quiete), esclusivamete deviatorico
τij = -pδij + σij Fluido in movimento
eij = 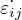 =
= 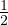 (
(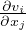 +
+ 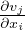 ) Velocitá di deformazione
) Velocitá di deformazione
τij = -pδij + 2η(eij -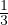 ekkδij) Fluido newtoniano di viscositá η
ekkδij) Fluido newtoniano di viscositá η
-
ρ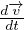 = ρ
= ρ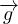 -∇p + η[∇2
-∇p + η[∇2
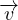 +
+ 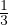 ∇(∇⋅
∇(∇⋅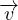 )] Equazione di Navier-Stokes
ρ
)] Equazione di Navier-Stokes
ρ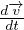 = ρ
= ρ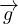 -∇p + η∇2
-∇p + η∇2
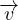 N-S per fluido incomprimibile (∇⋅
N-S per fluido incomprimibile (∇⋅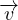 = 0)
ρ
= 0)
ρ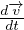 = ρ
= ρ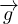 -∇p Equazione di Eulero, N-S per fluido inviscido (η = 0)
-∇p Equazione di Eulero, N-S per fluido inviscido (η = 0)
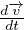 =
= 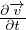 + ∇(
+ ∇(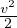 ) -
) -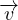 ×
×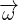 ρ(
ρ(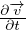 + ∇(
+ ∇(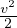 ) -
) -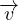 ×
×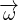 ) = ρ
) = ρ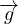 -∇p + η[∇2
-∇p + η[∇2
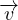 +
+ 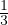 ∇(∇⋅
∇(∇⋅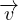 )] N-S in forma vettoriale
)] N-S in forma vettoriale
-
u(z) = 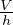 z, p(z) = ρg(h - z) + pa Flusso piano di Couette
z, p(z) = ρg(h - z) + pa Flusso piano di Couette
-
u(z) = 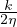 (h2 - z2) Flusso 1-D forzato da un gradiente di pressione(k)
(h2 - z2) Flusso 1-D forzato da un gradiente di pressione(k)
-
u(z) = 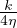 (R2 -r2) Flusso di Poiseuille, Flusso newtoniano in condotti cilindrici, max in r = 0
(R2 -r2) Flusso di Poiseuille, Flusso newtoniano in condotti cilindrici, max in r = 0
u = 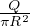 =
= 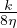 R2 =
R2 = 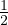 umax ∝ k Velocitá media del flusso in condotto, (Q portata)
umax ∝ k Velocitá media del flusso in condotto, (Q portata)
-
Transizione alla turbolenza
f = 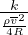 Fattore di attrito (forza di pressione/accelerazione)
Fattore di attrito (forza di pressione/accelerazione)
Re = 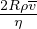 Numero di Reynolds (accelerazione/forza viscosa)
Numero di Reynolds (accelerazione/forza viscosa)
Transizione alla turbolenza quando Re > 2200 (sperimentale)
Per flusso laminare f = 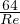
Per regime turbolento f = 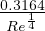 (sperimentale)
(sperimentale)
-
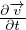 + ∇B =
+ ∇B = 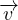 ×
×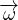 Teorema di Bernoulli (fluido inviscido)
B =
Teorema di Bernoulli (fluido inviscido)
B = 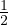 v2 + gz + ∫
v2 + gz + ∫ 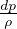 Funzione di Bernoulli
Funzione di Bernoulli
Flussi stazionari 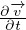 = 0
= 0
Flussi irrotazionali 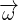 = ∇×
= ∇×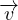 = 0
= 0
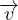 = ∇ϕ Potenziale di velocitá ϕ
= ∇ϕ Potenziale di velocitá ϕ
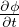 +
+ 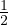 v2 + gz + ∫
v2 + gz + ∫ 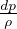 = 0 Teorema di Bernoulli per flusso inviscido irrotazionale
= 0 Teorema di Bernoulli per flusso inviscido irrotazionale
-
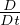 ∮
γ
∮
γ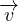 ⋅ d
⋅ d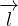 = 0 Teorema di Kelvin, dato un fluido inviscido barotropico in un sistema
inerziale la circuitazione di
= 0 Teorema di Kelvin, dato un fluido inviscido barotropico in un sistema
inerziale la circuitazione di 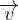 é costante nel tempo (non si formano vortici)
é costante nel tempo (non si formano vortici)
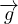 Legge di equilibrio idrostatico
Legge di equilibrio idrostatico
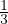 nmvrms2
nmvrms2
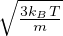
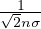 =
= 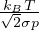 Libero cammino medio
Libero cammino medio
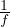 V v Deformazione pistone (f coefficiente di fluiditá, V v velocitá di deformazione)
V v Deformazione pistone (f coefficiente di fluiditá, V v velocitá di deformazione)
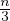 lmvrms =
lmvrms = 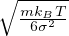 Viscositá dinamica [Pa s]
Viscositá dinamica [Pa s]
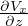 Sforzo di taglio per fluidi newtoniani (empirica)
Sforzo di taglio per fluidi newtoniani (empirica)
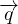 = -kT∇T Legge di Fourier
= -kT∇T Legge di Fourier
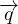 = -kT∇T = -
= -kT∇T = -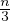 vrmslc∇T Legge Fourier per i gas (c calore specifico per molecola) da cui
kT =
vrmslc∇T Legge Fourier per i gas (c calore specifico per molecola) da cui
kT = 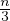 vrmslc =
vrmslc = 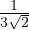
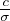 vrms ~ T
vrms ~ T
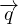 = -kT∇2T
= -kT∇2T
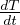 = DT∇2T con D
T diffusivitá termica DT =
= DT∇2T con D
T diffusivitá termica DT = 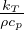 con cui stimiamo il tempo caratteristico
di conduzione τcond =
con cui stimiamo il tempo caratteristico
di conduzione τcond = 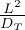
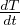 = DT∇2T =
= DT∇2T = 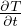 +
+ 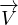 ⋅∇T dove
⋅∇T dove 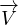 ⋅∇T é il termine avvettivo che ci permette di stimare
il tempo caratteristico di avvezione τavv =
⋅∇T é il termine avvettivo che ci permette di stimare
il tempo caratteristico di avvezione τavv = 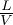
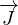 = -DF∇Φ Prima legge di Fick, J flusso di particelle, Φ concentrazione
= -DF∇Φ Prima legge di Fick, J flusso di particelle, Φ concentrazione
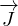 = -DF∇Φ = -
= -DF∇Φ = -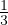 vrmsl∇Φ da cui DF =
vrmsl∇Φ da cui DF = 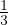 vrmsl che per il gas perfetto DF =
vrmsl che per il gas perfetto DF = 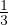 vrmsl =
vrmsl =
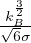
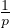
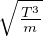
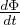 = DF∇2Φ Seconda legge di Fick che deriva dalla conservazione del numero di particelle
totali diffuse nel volume, da cui stimiamo il tempo caratteristico di diffusione τF =
= DF∇2Φ Seconda legge di Fick che deriva dalla conservazione del numero di particelle
totali diffuse nel volume, da cui stimiamo il tempo caratteristico di diffusione τF = 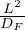
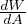 Tensione superficiale [Nm-1]
Tensione superficiale [Nm-1]
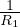 +
+ 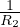 ) Legge di Laplace sulla curvatura delle superfici in discontinuitá di
pressione
) Legge di Laplace sulla curvatura delle superfici in discontinuitá di
pressione
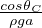 Legge di Yurin
Legge di Yurin
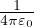
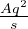 + Be-s∕δ Energia reticolare dove il primo termine é il termine attrattivo dato
dalla forza di Coulomb, A é la costante di Madelung determinata dalla geometria, s il passo
reticolare
+ Be-s∕δ Energia reticolare dove il primo termine é il termine attrattivo dato
dalla forza di Coulomb, A é la costante di Madelung determinata dalla geometria, s il passo
reticolare
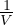
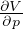 Compressibilitá
Compressibilitá
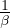 = -V
= -V 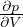 Incompressibilitá o "Bulk Modulus"
Incompressibilitá o "Bulk Modulus"
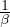 = -V
= -V 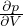 = V
= V 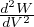 derivante da dW = -pdV
derivante da dW = -pdV
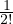 (
(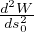 )Δs2+
)Δs2+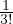 (
(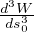 )Δs3+... = W0+
)Δs3+... = W0+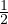 κΔs2-fΔs3+... sviluppo dell’energia
del reticolo
κΔs2-fΔs3+... sviluppo dell’energia
del reticolo
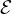 0 = W(s) + K = W0 +
0 = W(s) + K = W0 + 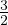 kBT
kBT
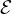 =
= 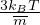 =
= 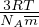 Energia totale di un atomo mediata sul reticolo per unitá di massa
Energia totale di un atomo mediata sul reticolo per unitá di massa
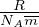 Legge di Dulong Petit dalla definizione di cv =
Legge di Dulong Petit dalla definizione di cv = 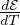
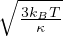 Passo d’oscillazione dell’atomo approssimando W(s) al secondo ordine, quindi
per oscillazione simmetrica
Passo d’oscillazione dell’atomo approssimando W(s) al secondo ordine, quindi
per oscillazione simmetrica
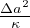 =
= 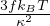 Dipendenza di epsilon dalla temperatura
Dipendenza di epsilon dalla temperatura
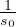
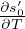 =
= 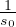
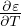 =
= 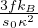 Coefficiente di espansione termica Lineare per un solido
Coefficiente di espansione termica Lineare per un solido
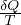 Secondo principio della termodinamica
Secondo principio della termodinamica
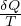 Secondo principio della termodinamica per processi reversibili
Secondo principio della termodinamica per processi reversibili
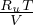
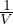
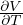

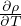
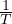 )
)
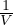
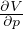

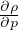
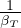
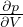
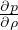
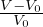
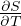
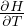
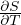
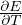
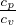
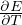
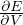
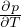
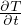
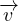
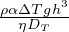
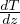
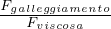
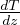
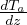
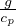 Gradiente adiabatico per gas perfetto
Gradiente adiabatico per gas perfetto
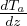
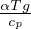 Gradiente adiabatico per sostanza generica
Gradiente adiabatico per sostanza generica
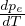
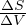 Equazione di Clausius-Clapeyron per la transizione di fase
Equazione di Clausius-Clapeyron per la transizione di fase
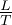 Variazione infinitesima di entropia dovuta al passaggio di fase
Variazione infinitesima di entropia dovuta al passaggio di fase
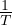
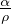
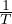
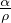
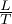
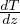
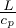
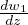 Gradiente termico in presenza di cambiamento di fase
Gradiente termico in presenza di cambiamento di fase
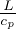
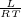 Pressione di vapor saturo lontano dalla T critica
Pressione di vapor saturo lontano dalla T critica
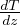
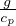
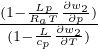
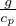
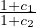
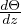
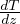
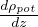
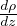
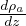
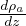 é il gradiente adiabatico
di densitá e
é il gradiente adiabatico
di densitá e 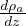
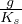 dove
dove 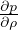
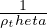

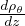
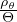
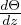
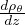
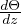
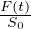
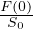
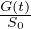
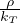
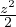
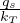
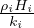
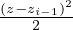
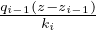
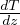
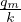
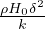
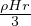 Flusso alla distanza
Flusso alla distanza 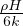
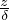
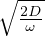 lo spessore di
penetrazione
lo spessore di
penetrazione
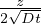
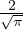
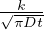
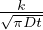
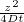 Flusso di calore del raffreddamento
istantaneo, ottenuto da
Flusso di calore del raffreddamento
istantaneo, ottenuto da 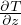
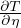
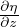 essendo
essendo 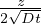
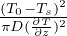
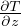 al flusso del raffreddamento istantaneo
al flusso del raffreddamento istantaneo
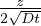

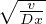
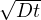
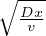 Spessore della Litosfera dato dall’aver compiuto il 90%
dell’escursione termica
Spessore della Litosfera dato dall’aver compiuto il 90%
dell’escursione termica
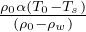
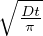 Topografia isostatica dei fondali oceanici (essendo
Topografia isostatica dei fondali oceanici (essendo 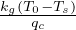 stima dell’altezza di un ghiacciaio trascurando avvezione e depositi di ghiaccio
(stima irrealistica), sono noti
stima dell’altezza di un ghiacciaio trascurando avvezione e depositi di ghiaccio
(stima irrealistica), sono noti 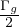
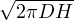
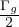
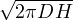
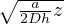
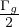
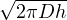
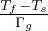
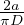 piú realisticamente
piú realisticamente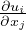
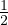
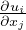
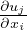
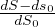 , viceversa con
, viceversa con 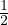
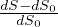
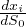
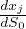 Variazione relativa di distanza fra due punti distanti
Variazione relativa di distanza fra due punti distanti 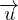
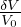 Traccia del tensore é variazione volumetrica relativa
Traccia del tensore é variazione volumetrica relativa
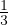
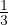
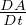
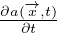
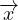
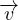
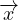
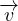 il flusso di
il flusso di 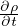
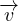
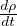
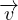
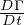
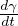
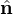
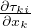
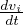 Equazioni del moto
Equazioni del moto
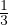
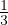
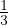
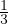
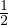
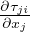 Stato di sforzo in prossimitá della superficie della crosta
Stato di sforzo in prossimitá della superficie della crosta
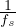 Teoria della fagliazione di Anderson avendo
Teoria della fagliazione di Anderson avendo 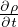
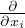
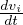
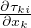
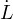
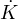
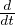
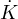
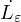 Equazione dell’energia per un continuo
Equazione dell’energia per un continuo
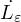
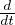
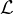
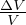 Lavoro speso per cambiare il volume
Lavoro speso per cambiare il volume
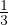
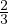
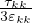
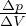
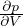
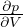
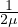
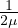
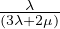
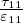
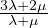 Modulo di Young, trazione su allungamento relativo
Modulo di Young, trazione su allungamento relativo
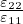
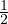
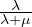 Modulo di Poisson, contrazione trasversale sulla variazione relativa
longitudinale
Modulo di Poisson, contrazione trasversale sulla variazione relativa
longitudinale
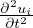
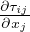 Equazione del moto per piccole deformazioni
Equazione del moto per piccole deformazioni
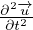
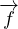
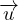
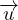 Equazione di Cauchy-Navier per le onde elastiche
Equazione di Cauchy-Navier per le onde elastiche
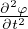
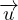
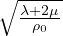 Velocitá onde P
Velocitá onde P
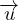 Onde S (
Onde S (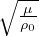 Velocitá onde S
Velocitá onde S
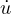 Pistone,
Pistone, 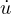 velocitá del pistone
velocitá del pistone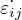
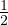
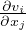
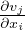
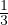
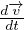
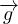
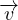
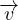 N-S per fluido incomprimibile (
N-S per fluido incomprimibile (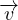
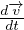
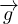
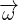
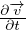
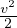
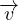
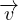
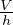
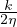
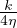
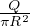
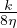
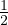
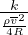 Fattore di attrito (forza di pressione/accelerazione)
Fattore di attrito (forza di pressione/accelerazione)
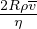 Numero di Reynolds (accelerazione/forza viscosa)
Numero di Reynolds (accelerazione/forza viscosa)
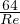
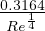 (sperimentale)
(sperimentale)
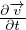
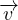
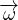 Teorema di Bernoulli (fluido inviscido)
Teorema di Bernoulli (fluido inviscido)
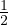
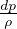 Funzione di Bernoulli
Funzione di Bernoulli
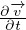
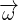
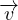
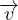
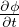
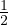
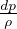
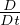
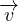
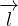
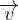 é costante nel tempo (non si formano vortici)
é costante nel tempo (non si formano vortici)