Sommario
Se non diversamente specificato, i due sistemi di riferimento sono presi tali per cui S sia fermo e
S’ si muova a velocitá 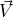 = V
= V 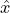 . c indica sempre la velocitá della luce. Le grandezze x0 indicano
misurazioni effettuate nel sdr con il corpo a riposo.
. c indica sempre la velocitá della luce. Le grandezze x0 indicano
misurazioni effettuate nel sdr con il corpo a riposo.
-
ds2 = dx2 + dy2 + dz2 - c2dt2 spazio di Minkowski
-
ds2 > 0 intervallo time-like: esiste un sdr in cui gli eventi avvengono nello stesso punto (in
tempi diversi). Possibile una reazione causa effetto tra i due
-
ds2 = 0 intervallo light-like: la luce puó viaggiare tra i due eventi. Relazione causa-effetto solo
tramite segnali luminosi
-
ds2 < 0 intervallo space-like: esiste un sdr in cui gli eventi avvengono simultaneamente (in
posti diversi)
-
xμ = (ct,x,y,z) = (ct,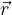 ) quadrivettore posizione
) quadrivettore posizione
-
ds2 = gμνdxμdxν notazione tensoriale, con gμν tensore metrico
-
xμ = gμνxν
-
vμ = (γc,γvx,γvy,γvz) = (γc,γ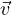 ) quadrivettore velocitá
) quadrivettore velocitá
-
aμ = γ(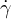 c,
c,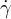
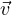 + γ
+ γ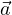 ) quadrivettore accelerazione
) quadrivettore accelerazione
-
aμ = (0,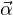 ) accelerazione propria
) accelerazione propria
-
pμ = m0vμ = (γm0c,γm0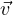 ) quadrivettore impulso (ogni componente si conserva
separatamente)
) quadrivettore impulso (ogni componente si conserva
separatamente)
-
fμ = 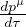 =
= 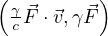 quadrivettore forza
quadrivettore forza
-
μ = 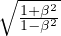 fattore di scala unitá spaziale di S’
fattore di scala unitá spaziale di S’
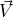 = V
= V 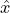 . c indica sempre la velocitá della luce. Le grandezze x0 indicano
misurazioni effettuate nel sdr con il corpo a riposo.
. c indica sempre la velocitá della luce. Le grandezze x0 indicano
misurazioni effettuate nel sdr con il corpo a riposo.
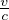
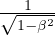
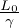 contrazione di Lorentz-FitzGerald
contrazione di Lorentz-FitzGerald
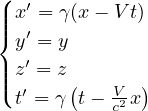
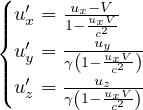
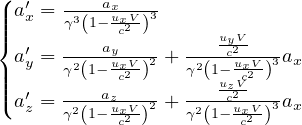
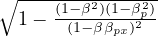 con
con 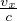
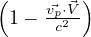
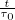 decadimento particellare
decadimento particellare
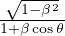 effetto Doppler con
effetto Doppler con 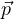
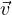
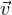 impulso relativistico
impulso relativistico
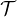
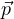
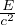
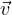
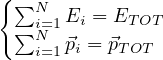
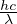
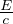
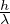
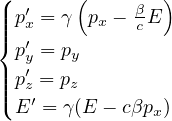
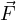
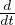
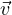
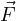
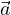
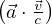
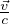

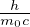
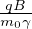 frequenza angolare di ciclotrone
frequenza angolare di ciclotrone
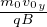 raggio di ciclotrone
raggio di ciclotrone
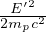 scontro tra protone fermo/in moto. E energia protone in moto. E’ energia finale
del sistema
scontro tra protone fermo/in moto. E energia protone in moto. E’ energia finale
del sistema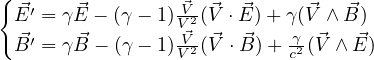
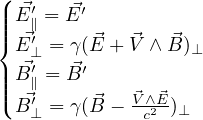
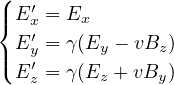
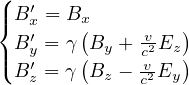
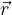
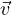
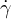
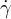
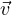
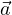
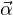
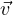
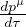
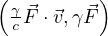 quadrivettore forza
quadrivettore forza
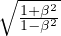 fattore di scala unitá spaziale di S’
fattore di scala unitá spaziale di S’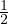
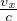
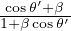 relativistic beaming, con
relativistic beaming, con 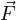
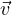 allora
allora 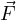
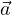
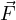
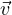 allora
allora 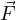
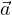
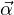
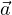
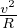
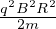 con R raggio acceleratore
con R raggio acceleratore