Guida esame ROOT
17 dicembre 2025
Sommario
Le notazioni utilizzate in questo schema sono 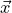 per rappresntare un generico array x, dim indica
sempre una dimensione, xCode indica un codice di root inerente a x, opt indica sempre la stringa
di caratteri che ROOT interpreta come opzioni, i indica un indice (o una quantitá indicizzabile),
n indica sempre un intero.
per rappresntare un generico array x, dim indica
sempre una dimensione, xCode indica un codice di root inerente a x, opt indica sempre la stringa
di caratteri che ROOT interpreta come opzioni, i indica un indice (o una quantitá indicizzabile),
n indica sempre un intero.
1 Istogrammi
TH1F("name", "title", nBins, xmin, xmax)
Dichiarazione di un istogramma 1D
-
Fill(x) o Fill(x, noccorrenze) fill del bin x
-
Draw("opt") per disegnare il grafico (E-barre errore, P-solo punti, SAME-sul grafico
precedente)
-
GetMean()
-
GetMeanError()
-
GetRMS() radice della varianza
-
GetRMSError()
-
GetMaximum() o GetMinimum()
-
GetEntries() numero di ingressi inseriti
-
Integral() come GetEntries ma non tiene conto dei pesi assegnati
-
Integral(bin1, bin2) integrale tra bin1 e bin2
-
GetIntegral() l’array dei conteggi cumulativi
-
Sumw2() imposta la somma in quadratura degli errori
Metodi dei bin:
-
GetMaximumBin() indice del bin contenente il valore massimo
-
GetBinCenter(ibin) centro del bin
-
GetBinContent(ibin) numero di elementi contenuti nel bin
-
GetBinContent(0) numero di UNDERFLOW
-
GetBinContent(nbin+1) numero di OVERFLOW
-
GetBinError(ibin)
-
SetBinContent(ibin, val) in y prende il valore val
Estetica:
-
SetMarkerStyle(markerCode)
-
SetMarkerSize(dim) setta la dimensione del marker a dim
-
SetFillColor(colorCode)
-
SetLineColor(colorCode)
-
GetXaxis()->SetTitle("name") setta il titolo dell’asse x (analogo per y)
-
GetYaxis()->SetTitleOffset(dim) offset del titolo
-
GetYaxis()->SetTitleSize(dim) dimensione carattere titolo
-
SetLineWidth(dim) spessore linea
Operazioni (sia h1 un istogramma):
-
n*h1 prodotto per lo scalare n
-
Divide(const *h1, const *h2, c1, c2, "opt") esegue la divisione (c1*h1)/(c2*h2). Di solito si
richiede l’opzione "B"
-
Add(const *h1, const *h2, c1, c2, "opt") esegue la somma c1*h1+c2*h2
2 Grafici
TGraph(npoints,
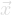
,
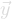
)
TGraph(filename, *format="%lg %lg", "opt")
da file TGraphErrors(n, x, y, ex, ey) grafico con barre errore TGraphErrors(filename, format="%lg %lg
%lg %lg", "opt")
-
Draw("opt") metodo per disegnare (A-disegna gli assi, P-disegna il marker dei punti, E-disegna
barre errore)
-
SetPoint(i, x, y) inserisce il punto (x,y) nella posizione i
-
GetPoint(i, x, y) assegna alle variabili (x,y) i valori del punto i
-
GetX() returna 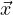 (analogo per y)
(analogo per y)
-
GetN() returna il numero dei punti
-
Integral() returna l’area sotto il grafico
-
GetCorrelationFactor()
-
GetCovariance()
Estetica:
-
SetTitle("title", "titleXaxis", "titleYaxis")
-
SetMarkerStyle(markerCode)
-
SetMarkerColor(colorCode)
-
SetLineColor(colorCode)
-
SetFillColor(colorCode)
3 Funzioni
TF1("name", "function", xmin, xmax)
nella funzione i parametri vanno indicati con [i]
NB: per funzioni definite a tratti, siano f(x) e g(x) funzioni generiche
"function" = "f(x)*(x>=a && x<b) + g(x)*(x>=b && x<c) + ..."
-
Draw()
-
SetParameter(i, value) setta il valore value al parametro iesimo
-
SetParameters(value1, value2, ..., valuen) setta il valore value i al parametro i
-
SetParLimits(i, xmin, xmax) definisce il range del parametro i
-
Eval(x) returna f(x)
-
Integral(a, b) integrale della funzione nel range [a,b]
-
DrawDerivative() grafica la derivata prima
-
DrawIntegral() grafica l’integrale
-
Derivative(x) o Derivative2(x) o Derivative3(x) calcola derivate
4 Fitting
Metodo Fit("name", "opt") valido per piú classi. Funzioni predefinite "gaus" "expo" "poln"
OptFit:
-
"R": usa il range della funzione (di default usa il range dell’istogramma)
-
"L": usa il metodo della massima verosimiglianza (default con chi-quadro)
-
"Q": stampa il minimo necessario dei risultati del fit
-
"V": stampa tutto quello che riesce dei risultati del fit
-
"S": ritorna risultati utili del fit
Metodi:
-
gStyle->SetOptFit(optCode) visualizza le info del fit
-
GetFunction(“f”) restituisce la funzione utilizzata nel fit (va utilizzata su un oggetto fittato)
-
GetChisquare()
-
GetNDF()
-
GetParameter(i) valore del parametro i-esimo
-
GetParError(i)
-
GetParameters(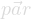 ) mette in
) mette in 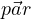 i parametri
i parametri
-
GetParErrors(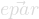 )
)
-
GetCorrelationMatrix() stampabile tramite Print()
-
GetCovarianceMatrix() stampabile tramite Print()
5 Random
gRandom->SetSeed()
per inizializzare la generazione Distribuzioni predefinite:
-
Uniform(a, b) uniforme in [a, b]
-
Rndm() uniforme in [0, 1]
-
Gaus(μ, σ)
-
Poisson(μ)
-
Binomial(ntot, prob)
-
Exp(τ) esponenziale decrescente
-
Integer(i) uniforme intera in [0, i-1]
-
Landau(moda, σ)
-
f1->GetRandom() genera un valore casuale dalla funzione f1
-
FillRandom("name", n) filla l’oggetto con n elementi della funzione "name"
6 Canvas
TCanvas("name", "title", "width", "height")
6.1 Legenda
TLegend(x1, y1, x2, y2, "name")
-
SetFillColor(n)
-
AddEntry(obj, "description") associa a obj una linea con descrizione
-
Draw("SAME") disegna la legenda sullo stesso grafico
7 List
TList()
-
Add(obj) con obj qualunque oggetto di root (TH1F, TF1, ...)
-
At(i) returna l’elemento i-esimo della lista. NB: returna sempre un TObject, al momento
dell’utilizzo specificarne il tipo con un static_cast<type>
-
Print() stampa a schermo la lista
-
At(i)->InheritsFrom("type") restituisce 1 se l’elemento i-esimo é di tipo type, 0 altrimenti
8 ROOT Files
TFile("name", "opt")
Options:
-
NEW o CREATE crea un nuovo file aperto in lettura, se giá esiste non si apre
-
RECREATE come CREATE ma se il file esiste lo sovrascrive
-
UPDATE apre un file esistente in scrittura, se non esiste lo crea
-
READ apre un file esistente in lettura (default)
Metodi:
-
TObject->Write() scrive sul file il TObject
-
Get("name") returna l’oggetto salvato di nome "name"
-
Close() chiude il file. Fondamentale inserirlo per evitare problemi
9 Benchmark
Metodi:
-
gBenchmark->Start("name") inizia un processo "name"
-
gBenchmark->Print("name") stampa le tempistiche in quel momento
-
gBenchmark->Show("name") interrompe il processo e ne stampa le tempistiche
-
gBenchmark->Stop("name") interrompe il processo "name"
10 Esempi
10.1 Lettura da file
ifstream in;
in.open("maxwell.dat"); //nome del file
Float_t x,y;
while (1) {
in >> x >> y;
if (!in.good()) break;
h1->Fill(y);
}
in.close();
10.2 Scrivere una classe su un ROOT File
In "MyClass.h"
Mettere inheritance: public TObject
Chiamare macro in fondo (prima della chiusura delle parentesi: ClassDef(MyClass, 1))
class MyClass: public TObject {
...
ClassDef(MyClass, 1) //rende la classe scrivibile sul file ROOT
};
In "MyClass.cxx"
Chiamare macro in fondo: ClassImp(MyClass)
Se hai fatto questo poi per scriverla sul file: //con A oggetto di MyClass
1) TFile *file = new TFile("test.root","recreate");
2) A.Write("A");
3) file->Close();
NB: per usare una classe esterna da ROOT:
gROOT->LoadMacro("MyClass.cxx++"); //compiling MyClass
10.3 Risoluzione o Smearing
10.3.1 A valore fisso
for(Int_t i=0;i<nGen;i++){
h[0]->Fill(gRandom->Gaus(fixedValue, res));
}
10.3.2 Con una distribuzione
for(Int_t i=0;i<nGen;i++){
h[1]->Fill(gRandom->Gaus(distribution, res));
}
10.4 Efficienza
10.4.1 Costante
(efficenza del 70%)
x=gRandom->Gaus(mean, sigma);
y=gRandom->Rndm();
if(y<0.7){h1->Fill(x)}
10.4.2 Variabile
TF1 *eff = new TF1(“eff”, "function", min, max);
x=gRandom->Gaus(mean, sigma);
y=gRandom->Rndm();
if(y < eff->Eval(x)) {
h1->Fill(x)
}
10.4.3 Istogramma dell’efficienza
TH1F *hEff=new Th1F(*hTot); //hTot istogramma con tutte le x(non solo quelle scartate)
hEff->Divide(h1, hTot, 1, 1, “B”); //h1 istogramma con solo le x accettate
10.5 Compilazione
10.5.1 da ROOT
.L macro.cpp oppure root [0] gROOT->LoadMacro(“macro.cpp”)
macro() [per eseguire]
10.5.2 da SHELL
g++ -o ExampleMacro .exe macro.cpp ‘root-config --cflags --libs‘
./macro.exe [per eseguire] //IMPORTANTE: la macro deve contenere un main()
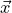 per rappresntare un generico array x, dim indica
sempre una dimensione, xCode indica un codice di root inerente a x, opt indica sempre la stringa
di caratteri che ROOT interpreta come opzioni, i indica un indice (o una quantitá indicizzabile),
n indica sempre un intero.
per rappresntare un generico array x, dim indica
sempre una dimensione, xCode indica un codice di root inerente a x, opt indica sempre la stringa
di caratteri che ROOT interpreta come opzioni, i indica un indice (o una quantitá indicizzabile),
n indica sempre un intero.
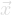 ,
, 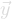 )
)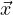 (analogo per y)
(analogo per y)
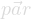 )
)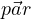 i parametri
i parametri
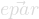 )
)