β = 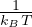
Z1 = ∑ se-βϵs funzione di partizione (particella singola)
Z = (Z1)N funzione di partizione (N particelle distinguibili)
Z = 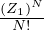 funzione di partizione (N particelle indistinguibili nel limite diluito)
funzione di partizione (N particelle indistinguibili nel limite diluito)
F = -kBT lnZ energia libera di Helmoltz
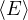 =
= 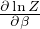 energia media
energia media
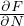
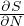
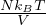
![[ (nQ) 5]
ln n + 2](b_formulario_materia7x.png) equazione di Sackur-Tetrode
equazione di Sackur-Tetrode
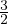
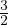
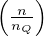
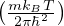
 concentrazione quantistica
concentrazione quantistica
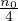
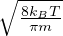 legge di Graham (effusione)
legge di Graham (effusione)
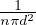 libero cammino medio
libero cammino medio
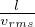 tempo medio di collisione
tempo medio di collisione
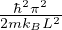 temperatura caratteristica traslazioni
temperatura caratteristica traslazioni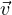
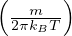

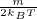
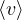
 velocitá media
velocitá media
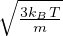 velocitá quadratica media
velocitá quadratica media
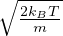 velocitá piú probabile
velocitá piú probabile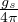
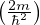

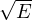 occupazione media per lv energetico (3D)
occupazione media per lv energetico (3D)
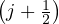 energia oscillatore armonico quantistico
energia oscillatore armonico quantistico
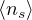
![[ β(μ- ϵs)]
1+ e](b_formulario_materia32x.png)
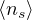
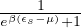 distribuzione di Fermi-Dirac
distribuzione di Fermi-Dirac
![[---1----]
1-eβ(μ-ϵs)](b_formulario_materia35x.png)
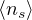
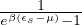 distribuzione di Bose-Einstein
distribuzione di Bose-Einstein
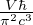
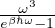
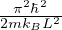 temperatura caratteristica di traslazione (1D)
temperatura caratteristica di traslazione (1D)
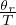 funzione di partizione per d.o.f. rotazionali
funzione di partizione per d.o.f. rotazionali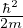
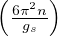
 energia di Fermi
energia di Fermi
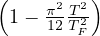
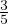
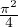
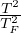
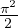
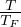
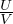
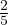
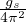

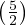
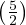
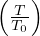
 (
(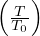
 (
(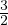
![[ ]
1- ζ(325)(T0) 32 + ...
22 T](b_formulario_materia64x.png) (
(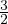
![[1+ 0.231(T0)32 + ...]
T](b_formulario_materia66x.png) (
(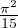
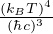
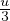
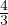
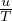
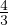
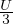
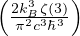
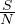
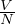
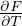
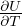
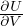
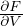
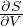
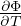
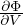
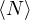
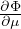
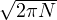
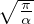 integrale gaussiano
integrale gaussiano
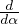
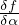
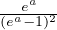
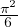
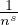 funzione zeta di Riemann
funzione zeta di Riemann
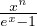
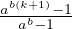
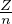
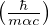
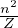
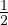
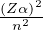
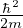
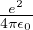

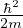
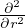
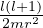
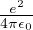

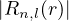
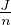
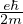 magnetone di Bohr
magnetone di Bohr
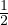
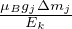
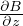
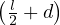 spostamento da Stern-Gerlach
spostamento da Stern-Gerlach
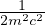

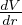
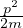
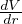
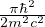
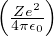
![[1+ (Zα)2( -n-- 3)]
n2 j+ 12 4](b_formulario_materia127x.png) correzione totale
correzione totale