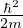fe(e)de = 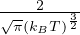 e-
e-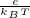 e
e de distribuzione energia di Maxwell
de distribuzione energia di Maxwell
S = NkB![[ ]
lnT + ln 2πkωB-+ 1](b_formulario_meccanica_quantistica3x.png) entropia gas di oscillatori armonici
entropia gas di oscillatori armonici
zωCN = αωCNzωx legge di Kirchhoff
P = 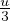 equazione di stato corpo nero CN
equazione di stato corpo nero CN
z = ∫ 0∞dωzω = σT4 legge di Stefan-Boltzmann
uω = 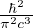
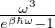 legge di Planck
legge di Planck
Relazioni di Plank-Einstein:
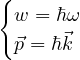 |
λdB = 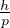 lunghezza d’onda di deBroglie
lunghezza d’onda di deBroglie
Δλf = 2λC sin2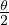 legge di Compton
legge di Compton
λn,m = R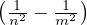 formula di Rydberg per l’idrogeno (n < m)
formula di Rydberg per l’idrogeno (n < m)
λa,b,n,m = R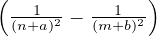 formula di Rydberg per il sodio
formula di Rydberg per il sodio
R = 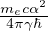 costante di Rydberg
costante di Rydberg
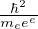 raggio di Bohr
raggio di Bohr
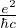
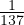 costante di struttura fine
costante di struttura fine
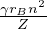 con
con 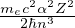
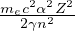
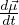
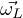
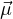
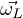
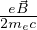 frequenza angolare di Larmor
frequenza angolare di Larmor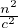
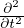



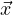
![[ 2 ]
⃗p ⋅ dd⃗qt - p2m-- U(⃗q)](b_formulario_meccanica_quantistica30x.png) funzione di Hamilton
funzione di Hamilton
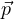

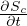
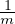


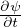
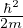
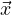
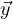
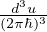
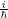
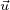
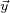
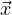
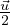
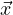
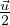
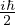
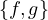
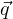
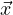 posizione
posizione
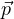
 quantitá di moto
quantitá di moto
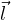
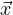
 momento angolare
momento angolare